Comparing Recursive and Iterative Algorithms: Binary Search and Factorial

I'm in the middle of putting together a new course for our undergraduates at Cardiff University. The course is called 'Computing for Mathematics' and will introduce our first year students to programming in general (using python) as well as how a mathematics package can help them during there degree (we'll be using +Sage Mathematical Software System which is a natural extension from python and is also super awesome).

I was prepping some stuff on recursion (which I'm really looking forward to teaching to our mathematics students given the connection to induction) and came across a bunch of posts stating the lack of speed generally associated to recursion:

• Stack overflow question
• Speed vs elegance
• Nothing to do with any of this

I thought I'd write some (python) code to see how much slower recursion was. All the code (and data) is in this github repo.

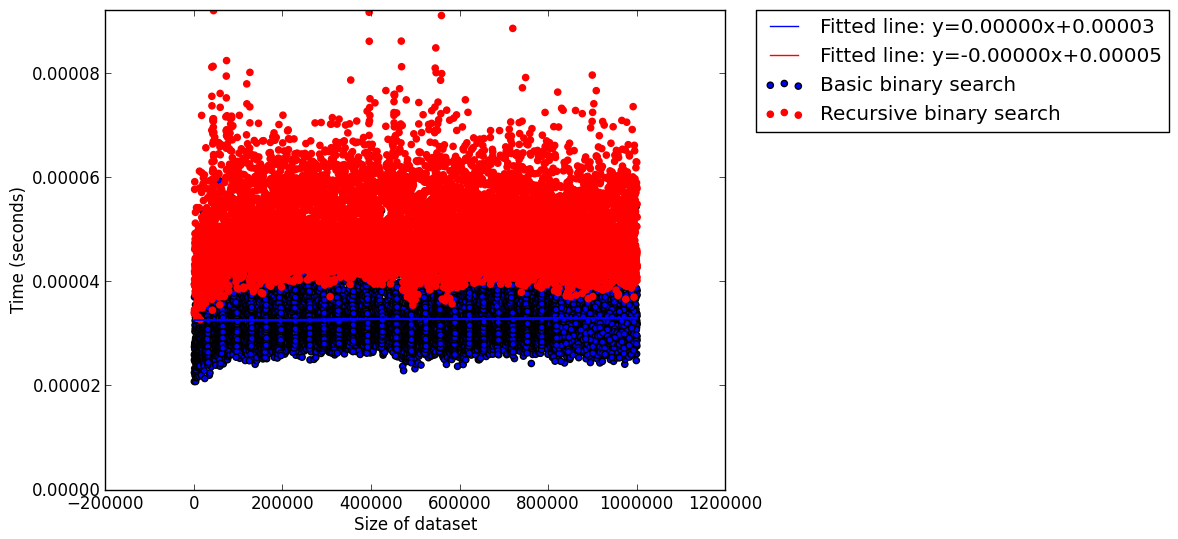
Binary search

The first algorithm I thought I'd take a look at was binary search. I tried to write each algorithm in as basic a way as possible so as to allow for the best possible comparison.

Iterative

Here's the algorithm written iteratively:

def iterativebinarysearch(target):
    """
    Code that carries out a binary search
    """
    first = 0
    last = len(data)
    found = False
    while first <= last and not found:
        index = int((first + last) / 2)
        if target == data[index]:
            found = True
        elif target < data[index]:
            last = index - 1
        else:
            first = index + 1
    return index

Recursive

And here's the algorithm written recursively:

def recursivebinarysearch(target, first, last):
    """
    Code that carries out a recursive binary search
    """
    if first > last:
        return False
    index = int((first + last) / 2)
    if target == data[index]:
        return index
    if target < data[index]:
        return recursivebinarysearch(target, first, index - 1)
    else:
        return recursivebinarysearch(target, index + 1, last)
    return index

The experiment

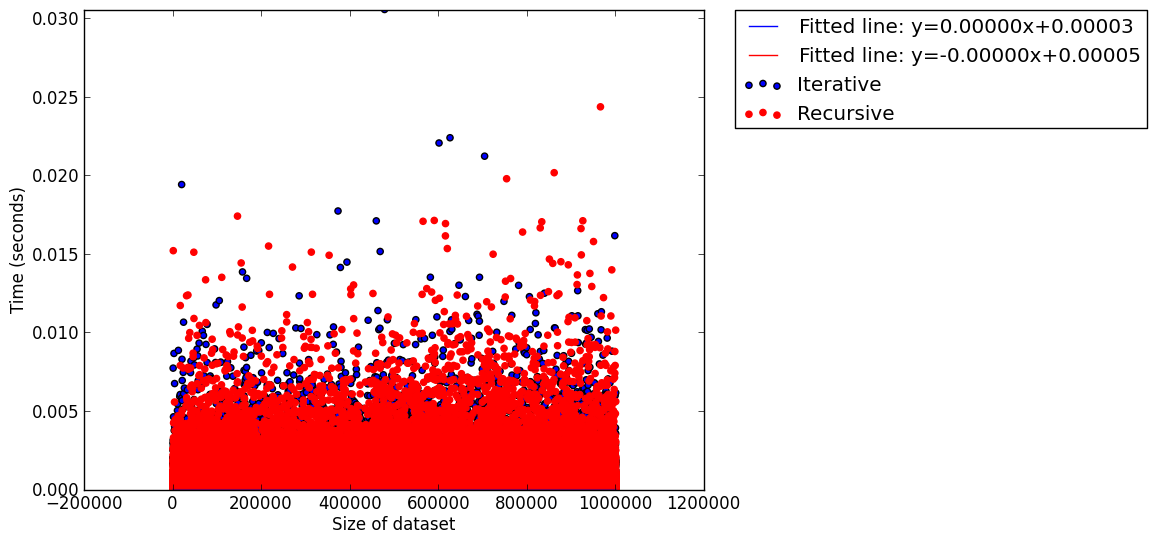
I timed 10 runs of each of these algorithms on data sets of varying size, for each size choosing a random 1000 points to search. The data is all available in this github repo.

Here's a scatter plot (with fitted lines) for all the data points:

A part from the fact that binary search seems very good indeed, there's not that much going on here apart from perhaps a slight tendency for iterative approach to be a bit slower.

I decided to take a look at the mean time (over the 1000 searches done for each data set):

This seems to show that the iterative approach is slow but again it's not very clear. This is mainly due to the fact that I haven't done any clever analysis. The data sets are pretty big (10,001,000 data points plotted in the 1st graph and 10,001 in the 2nd) so to do anything really useful I'd have to take a look at the data a bit more carefully (the two csv files: 'recursivebinarysearch.csv' and 'iterativebinarysearch.csv' are both on github).

I thought I'd try a 'simpler' algorithm as there are perhaps a bunch of things going on with the binary search (size of data set, randomness of points chosen etc...).

Computing Factorial

The other algorithm I decided to look at was the very simple calculation of $n!$.

Iteration

Here's the simple algorithm written iteratively:

def iterativefactorial(n):
    r = 1
    i = 1
    while i <= n:
        r *= i
        i += 1
    return r

Recursion

Here's the algorithm written recursively:

def recursivefactorial(n):
    if n == 1:
        return 1
    return n * recursivefactorial(n - 1)

The experiment

This was a much easier experiment to analyse however as the timings increased I thought it would also be interesting to look at the ratio of the timings:

We see that first of all the iterative algorithm seems to perform better but as the size of $n$ increases we notice that this improvement is not as noticeable. My computer maxed out it's stack limit  so I won't be checking anything further but I wonder if the ratio would ever get bigger than 1... (This data set: 'factorial.csv' is also on github).

I'm sure that there's nothing interesting in all this from a computer scientists point of view but I found it a fun little exercise :)