This is a great paper.
Firstly there is a nice definition of what active learning is:
"Active learning engages students in the process of learning through activities and/or discussion in class, as opposed to passively listening to an expert. It emphasizes higher-order thinking and often involves group work."The definition given in the paper for a traditional lecture is given as:
"[...] student activity is assumed to be limited to taking notes and/or occasional and unprompted questions of the instructor."The definition for active learning is not obtained out of thin air but takes in to account over 300 audience members at departmental seminars on active learning throughout North America.
What I particularly like about the definition is that it specifically makes a point of mentioning the higher-order thinking.
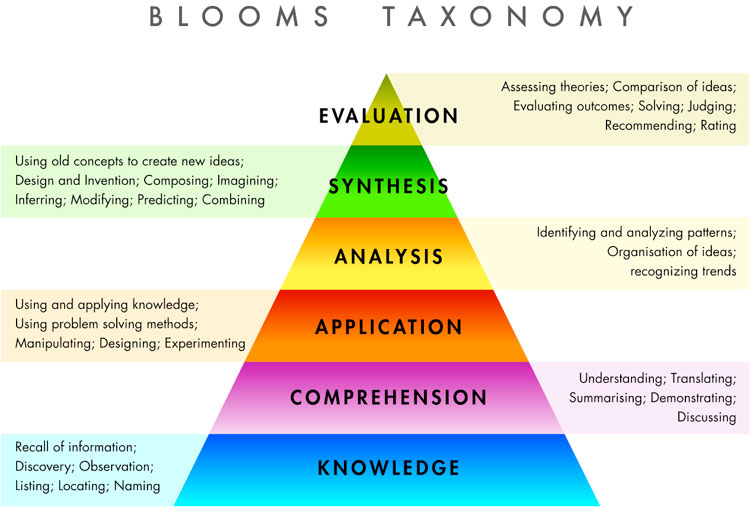
I was recently lucky enough to attend a talk by Dr. Collin Jones who teaches in Tasmania using an active learning approach. Here is a diagram that I've put together trying (humbly) to get across what he said on the subject of active learning (you might want to open the image in a new tab...):
In that I'm trying to say that if we want students to access the higher levels of Bloom's taxonomy across the various topics in a course, with our help through contact time then a more active learning approach seems logical.
It looks like Freeman's paper confirms this.
The first section quickly summarsies the findings of rigorously (as far as I can tell the rigour in this paper is great) analysing the results of 225 studies that obeyed the following criteria:
- Involved a comparison between traditional lecturing and active learning;
- Involved a regular class;
- Only looked at comparison where the delivery method was the main change;
- Involved a STEM subject;
- Included an evaluation of academic performance
There are a variety of well presented findings and I will try and summarise them very briefly here:
- Students will perform by just under half a standard deviation better in an active learning environment;
- Students are 1.5 times more likely to fail in a traditional lecture environment;
- 1. and 2. are not affected by the particular STEM subject;
- The gain in 1. for concept inventory style assessment are lower than for 'instructor-written' type assessment. This is argued (and I think I agree) to be in line with my arrows going through Bloom's taxonomy. In an active learning environment students are more likely to perform well on tasks that require a deeper learning;
- The gain in 1. is more prominent in smaller classes. This also makes sense (taking a class with a minimum number of students of 1, it would be idiotic to lecture and similarly for an infinite class perhaps an active learning approach would not be appropriate).
Evidence
+Stan Yoshinobu has written a brief post about Freeman's paper at The IBL blog and I really like:
"The perspective I like to take is one that is used in medicine. When new techniques or treatments are shown through evidence to provide better care for patients, then the medical community adopts those new practices."This is something alluded to by Freeman et al. They talk about their paper (and others) being the 'first generation' of research in to active learning and that now that there is evidence for the benefits perhaps the second generation of research would start looking at best types of active learning for given students etc...
1 last thing.
The final thing I want to talk about is the potential weakness of this research. This is pointed out by the authors:
"The instructors who implemented active learning in these studies did so as volunteers. It is an open question whether student performance would increase as much if all faculty were required to implement active learning approaches."My personal opinion is that that really hits the issue on the head. Instructors who innovate with their teaching so as to move away from the tried and tested lecture that has been in place for 100s of years are most probably the academics who have the energy and conviction to put a lot of effort in to their teaching.
Often in academia where the pressure to publish and obtain funding are immense it is sad to say that it's very easy to simply reach for the same set of notes that has always passed down and lecture. This leaves students to attempt to reach deeper levels of learning on their own.
It must also be said though, (as alluded to in the paper) active learning means a variety of things. For example I use problem based learning, flipped classrooms and a combination of active game playing (that I would like to think has some element of inquiry based learning) in my own teaching however active learning in Freeman's paper has a breadth of meanings which include the simple use of clickers to get some form of student engagement with the learning. So I don't necessarily think that an active learning approach implies a huge distancing from classic lecturing for all instructors (see the earlier definitions of the active learning and traditional lecture).
As the authors' state it's a case of now identifying the best pedagogic approaches for instructors as well as students: getting that pairing right.
Fun
I really enjoyed something that Dr Sue Rigby said at the opening of the 2014 HEA STEM conference:
"We have to teach in a way that is fun. We get to choose how we teach"As educators I think it's very important to remember that we do indeed get to choose how we teach and ultimately active learning is often simply far more fun than traditional lectures (I sure had a smile on my face when trying to teaching cooperative game theory by having students play waste paper basketball).
We should always choose a pedagogic approach for a better reason than "that's how it has always been done". Sound research like the one in this paper seems like a good a reason as any.
-----
Edit: On the 7 and 8th of July (2014) +Paul Harper and I are hosting a workshop on active learning techniques. Please take a look :)